
Cùng mục freesoftware.vn tìm hiểu Tổng hợp các Bộ đề thi học kì 1 môn Toán lớp 6 năm 2022 – 2023 Có đáp án , đề kiểm tra học kì 1 lớp 6 môn Toán (Có ma trận) nhé!
Đề thi học kì 1 môn Toán 6 năm 2022 – 2023
| PHÒNG GIÁO DỤC HUYỆN…..
TRƯỜNG TH&THCS…… |
ĐỀ KIỂM TRA HỌC KÌ I NĂM 2022 – 2023 MÔN TOÁN 6 Thời gian làm bài: 90 phút |
PHẦN 1. TRẮC NGHIỆM
Chọn đáp án đúng.
Câu 1. 38 đọc là:
A. Tám mũ ba
B. Ba mũ tám
C. Tám nhân ba
D. Ba nhân tám
Câu 2: Số nguyên chỉ năm có sự kiện “Thế vận hội đầu tiên diễn ra năm 776 trước công nguyên” là số nào trong các số sau đây?
A. – 1776
B. 776
C. – 776
D. 1776
Câu 3. Hình nào dưới đây là hình tam giác đều?

Câu 4: Hình nào dưới đây có trục đối xứng?
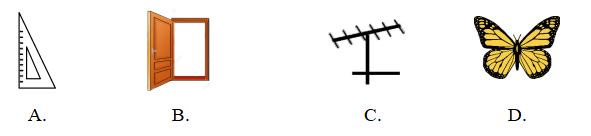
PHẦN 2. TỰ LUẬN
Câu 5: Trong các số 1930, 1945, 1954, 1975. Những số nào chia hết cho 5? Vì sao?
Câu 6: Một chiếc tàu ngầm đang ở độ cao -47 m so với mực nước biển. Sau đó tàu ngầm nổi lên 18 m.
a) Viết phép tính biểu thị độ cao mới của tàu ngầm so với mực nước biển.
b) Tính độ cao mới của tàu ngầm so với mặt nước biển.
Câu 7: Bản tin dự báo thời tiết dưới đây cho biết nhiệt độ thấp nhất và nhiệt độ cao nhất ở Thủ đô Mát-xcơ-va của Liên bang Nga (tính theo độ C) trong các ngày từ 17/1/2021 đến 23/1/2021
a) Nêu nhiệt độ cao nhất, nhiệt độ thấp nhất ở Thủ đô Mát-xcơ-va của Liên bang Nga (tính theo độ C) trong ngày 22/1/2021
b) Chênh lệch giữa nhiệt độ cao nhất và nhiệt độ thấp nhất ở Thủ đô Mát-xcơ-va của Liên bang Nga trong ngày 22/1 2021 là bao nhiêu độ C ?

Câu 8:
a) Tìm bội chung nhỏ nhất của 18 và 27.
b) Thực hiện phép tính:
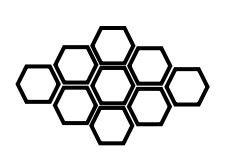
Câu 9: Dùng thước và compa vẽ hình thoi ABCD biết cạnh AB = 3cm, đường chéo AC = 5cm.
Đáp án đề thi học kì 1 môn Toán 6 năm 2021 – 2022
Câu 1:
– Để trả lời được câu một học sinh phải đọc được biểu thức lũy thừa của một số tự nhiên.
– Câu 1 đánh giá năng lực giao tiếp toán học theo mức độ 1.
– Đáp án: B.
– Điểm số: 0,5.
Câu 2:
– Để trả lời được câu 2, học sinh phải biết sử dụng số nguyên âm để chỉ thời gian trước Công nguyên.
– Câu 2 đánh giá năng lực mô hình hóa toán học theo mức 1.
– Đáp án: C.
– Điểm số: 0,5.
Câu 3:
– Để trả lời được câu 3 học sinh phải nhận biết được tam giác đều.
– Câu 3 đánh giá năng lực tư duy và lập luận toán học theo mức 1.
– Đáp án D.
– Điểm số: 0,5.
Câu 4:
– Để trả lời được câu 4 học sinh phải nhận biết được hình phẳng có trục đối xứng.
– Câu 4 đánh giá năng lực tư duy và lập luận toán học theo mức 1.
– Đáp án: A.
– Điểm số 0,5.
Câu 5:
– Để trả lời được câu 5 học sinh phải biết dựa vào dấu hiệu chia hết cho 5.
– Câu 5 đánh giá năng lực tư duy và lập luận toán học theo mức 2.
– Giải: Trong các số 1930, 1945, 1954, 1975, những số chia hết cho 5 là: 1930, 1945, 1975, vì chúng có chữ số tận cùng là 0 ; 5
– Điểm số: 1,5
Câu 6:
a)
– Để làm được câu 6a, học sinh phải hiểu được vấn đề thực tiễn gắn với thực hiện các phép tính số nguyên.
– Câu 6a đánh giá năng lực mô hình hóa toán học theo mức 2.
– Giải: Phép toán liên quan đến độ cao mới của tàu ngầm dưới mực nước biển là: -47 + 18.
– Điểm số: 0,5
b)
– Để làm được câu 6b học sinh phải giải quyết được vấn đề thực tiễn gắn với thực hiện các phép tính số nguyên.
– Câu 6b đánh giá năng lực mô hình hóa toán học theo mức 3.
– Giải: Độ cao mới của tàu ngầm so với mực nước biển là: -47 + 18 = -29 (m).
– Điểm số: 0,5
Câu 7:
a)
– Để trả lời được câu 7a, học sinh phải hiểu được vấn đề thực tiễn gắn với so sánh hai số nguyên.
– Câu 7a đánh giá năng lực mô hình hóa toán học theo mức 2.
– Giải:
+ Nhiệt độ cao nhất ở Thủ đô Mát-xcơ-va của Liên bang Nga tính theo độ C trong ngày 22/1/2021 là: -1 0C.
+ Nhiệt độ thấp nhất ở Thủ đô Mát-xcơ-va của Liên bang Nga tính theo độ C trong ngày 22/1/2021 là: -9 0C.
– Điểm số: 1.
b)
– Để trả lời được câu 7b, học sinh phải giải quyết được vấn đề thực tiễn gắn với thực hiện các phép tính số nguyên.
– Câu 7b đánh giá năng lực mô hình hóa toán học theo mức 3.
– Giải:
Chênh lệch giữa nhiệt độ cao nhất và nhiệt độ thấp nhất ở Thủ đô Mát-xcơ-va của Liên bang Nga trong ngày 22/1/2021 là: -1 – (-9) = 8 0C.
– Điểm số: 0,5
Câu 8:
a)
– Để làm được câu 8a, học sinh phải xác định được bội chung nhỏ nhất của hai số tự nhiên.
– Câu 8a, đánh giá năng lực giải quyết vấn đề toán học theo mức 3.
– Giải:
Phân tích 18 và 27 ra thừa số nguyên tố:
18 = 2 . 3 . 3 = 2 . 32
27 = 3 . 3 . 3 = 33
BCNN(18, 27) = 2 . 32 = 2 . 27 = 54
– Điểm số: 1.
b)
– Để làm được câu 8b, học sinh phải thực hiện được phép cộng phân số bằng cách sử dụng bội chung nhỏ nhất.
– Câu 8b đánh giá năng lực giải quyết vấn đề toán học theo mức 3.
– Giải:
BCNN(18, 27) = 54
54 : 18 = 3
54 : 27 = 2
– Điểm số: 1.
Câu 9:
– Để làm được câu 9, học sinh phải biết các bước vẽ hình thoi khi biết độ dài cạnh và độ dài một đường chéo.
– Câu 9 đánh giá năng lực sử dụng công cụ, phương tiện học toán theo mức 3.
– Giải: (Học sinh không cần trình bày các bước vẽ trong bài làm của mình). Kết quả vẽ được như hình bên.
– Điểm số: 1.
Câu 10:
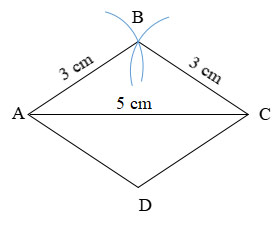
– Để làm được câu 10 học sinh phải coi mỗi đoạn ống hút biểu diễn một cạnh của lục giác đều, mô tả được một số yếu tố cơ bản của lục giác đều, biết cách tạo lập lục giác đều.
– Câu 10 đánh giá năng lực mô hình hóa toán học, giải quyết vấn đề toán học mức 4.
– Giải:
a) Muỗi hút được cắt thành 3 đoạn bằng nhau để tạo nên ba cạnh của mỗi lục giác đều.
Vậy mỗi lục giác đều cần 2 ống hút.
Trên hình có tất cả 9 lục giác đều, do đó số hút mà bạn Hoa đã sử dụng là:
9 . 2 = 18 (ống hút).
b) Tổng chiều dài của tất cả các ống hút mà bạn Hoa đã dùng là:
18 . 198 = 3564 (mm)
– Điểm số: 1.
Ma trận đề thi học kì 1 môn Toán 6 sách Chân trời sáng tạo
| Nhận biết | Thông hiểu | Vận dụng | vận dụng cao | Cộng | |||||
| TN | TL | TN | TL | TN | TL | TN | TL | ||
| Chương 1. Số tự nhiên. | |||||||||
| Số câu | 1 | 1 | 2 | 4 | |||||
| Số điểm | 0,5 | 1,5 | 2 | 4 | |||||
| Số câu/ Hình thức | 1 | 5 | 8a, 8b | ||||||
| Thành tố năng lực. | GT | TD | GQVĐ | ||||||
| Chương 2. Số nguyên. | |||||||||
| Số câu | 1 | 2 | 2 | 5 | |||||
| Số điểm | 0,5 | 1,5 | 1 | 3 | |||||
| Số câu/ Hình thức | 2 | 6a, 7a | 6b,7b | ||||||
| Thành tố năng lực. | MHH | MHH | MHH | ||||||
| Chương 3. Hình học trực quan. | |||||||||
| Số câu | 2 | 1 | 2 | 5 | |||||
| Số điểm | 1 | 1 | 1 | 3 | |||||
| Số câu/ Hình thức | 3,4 | 9 | 10a, 10b | ||||||
| Thành tố năng lực. | TD | CC | MHH, CC, GQVĐ | ||||||
| Tổng điểm | 2 | 3 | 4 | 1 | 10 | ||||
Đề thi học kì 1 môn Toán 6 năm 2022 – 2023 sách Kết nối tri thức với cuộc sống
Ma trận đề thi học kì 1 môn Toán 6 năm 2022 – 2023
| TT | Nội dung kiến thức | Đơn vị kiến thức | Mức độ nhận thức | Tổng | % tổng điểm | |||||||||
| Nhận biết | Thông hiểu | Vận dụng | Vận dụng cao | |||||||||||
| Số CH | TG (phút) | |||||||||||||
| Số CH | TG (phút) | Số CH | TG (phút) | Số CH | TG (phút) | Số CH | TG (phút) | TN | TL | |||||
| 1 | Chương I | 1.1.Tập hợp- ước chung | 1 | 3 | 1 | 0 | 3 | 15% | ||||||
| 1.2.Lũy thừa với số mũ tự nhiên | 1 | 2 | 1
|
5 | 1 | 1 | 7 | |||||||
| 2
|
Chương II
|
2.1.Quan hệ chia hết -tính chất- số nguyên tố | 2 | 4 | 2 | 0 | 4 | 30% | ||||||
| 2.2. Ước chung- Bội chung | 1
|
15 | 1 | 15 | ||||||||||
| 3
|
Chương III
|
3.1.Các phép tính cộng- trừ- nhân- chia số nguyên | 1 | 3 | 4
|
25
|
|
4
|
28 | 35% | ||||
| 3.2.Phép chia hết, ước và bội của một số nguyên | 1
|
20 | 1 | 20 | ||||||||||
| 4 | Chương IV | 4.1.Một số hình học phẳng (Hình bình hành) | 1 | 3 | 1 | 0 | 3 | 20% | ||||||
| 4.2.Chu vi và diện tích của một số loại tứ giác | 1
|
10 | 1 | 10 | ||||||||||
| Tổng | 6 | 15 P | 6 | 40P | 1 | 15P | 1 | 20P | 6 | 8 | 90P | |||
| Tỉ lệ (%) | 30% | 40% | 20% | 10% | 100% | |||||||||
| Tỉ lệ chung (%) | 70% | 20% | 10% | |||||||||||
Bảng đặc tả đề kiểm tra cuối học kì 1 môn Toán 6
| TT | Nội dung kiến thức | Đơn vị kiến thức | Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá | Số câu hỏi theo mức độ nhận thức | Tổng | |||
| Nhận biết | Thông hiểu | Vận dụng | Vận dụng cao | |||||
| 1 | Chương I | 1.1.Tập hợp- ước chung | Nhận biết: Cách viết một tập hợp, ước chung ( câu 1- TN) | 1 | 1 | |||
| 1.2.Lũy thừa với số mũ tự nhiên | Nhận biết: Hiểu cách nhân hai lũy thừa cùng cơ số. (câu 2- TN)
Thông hiểu: cách chia hai lũy thừa cùng cơ số ( câu 1- TL ý b) |
1 | 1 | 2
|
||||
| 2 | Chương II | 2.1.Quan hệ chia hết -tính chất- số nguyên tố | Nhận biết:
– Nhận biết một tổng chia hết cho 5 khi các số hạng đều chia hết cho 5 (câu 3- TN) – Nhận biết một số là số nguyên tố ( Câu 5-TN) |
2 | 2 | |||
| 2.2. Ước chung- Bội chung | Vận dụng: Vận dụng cách tìm ƯC LN để giải toán ( câu 3-TL) | 1 | 1 | |||||
| 3 | Chương III | 3.1.Các phép tính cộng- trừ- nhân- chia số nguyên | Nhận biết: Tính chất của phép cộng số nguyên ( câu 6 –TN)
Thông hiểu: hiểu được Hiểu được các quy tắc, các tính chất của các phép tính để thực hiện các phép tính.(Câu 1- TL ý a,c; câu 2- TL ý a,b) |
1 | 4 |
5
|
||
| 3.2.Phép chia hết, bội và ước của một số nguyên | Vận dụng: Phép chia hết, bội và ước của một số nguyên ( câu 5-TL) | 1 | 1
|
|||||
| 4 | Chương IV | 4.1.Một số hình học phẳng | Nhận biết: Tính chất Hình bình hành.( câu 4- TN) | 1 | 1
|
|||
| 4.2.Chu vi và diện tích của một số loại tứ giác | Hiểu: Công thức tính diện tích hình thang, cách đổi đơn vị ( câu 4- TL) | 1 | 1 | |||||
| Tổng | 6 | 6 | 1 | 1 | 14 | |||
Đề thi học kì 1 môn Toán 6 năm 2022 – 2023
I. Trắc nghiệm: (3,0 điểm)
Khoanh tròn chữ cái đứng trước phương án trả lời đúng trong các câu sau đây:
Câu 1. Cách viết nào sau đây là đúng. Tập hợp các ƯC (24; 16) là: A = {1; 2; 4; 8}.
A. 1 ∉ A
B. {2; 4} ⊂ A
C. 8 ⊂ A
D. 4 ∉ A
Câu 2. Phép nhân 2.2.2.2.2.2 được viết thành
A. 2
B. 26
C. 62
D. 23
Câu 3. Không thực hiện phép tính, tổng nào sau đây chia hết cho 5
A. 15+ 2021
B. 2020 + 2022
C. 2020 + 2025 + 2030
D. 2020 + 2025 + 2029
Câu 4.Trong hình bình hành nhận xét nào sau đây là sai?
A. Các cạnh đối bằng nhau
B. Các góc đối bằng nhau
C. Hai đường chéo vuông góc
D. Các cạnh đối song song với nhau
Câu 5. Cho các số: 6; 13 ; 26; 35 trong đó số nguyên tố là:
A. 6
B. 13
C. 26
D. 35
Câu 6. Chọn câu đúng nhất: Phép cộng số nguyên có các tính chất:
A. Giao hoán và kết hợp
B. Giao hoán
C. Kết hợp
D. Một đáp án khác
II. Tự luận: (7,0 điểm)
Câu 1: (1,5 điểm) Tính
a) 79 – (79 – 2021)
b) 45: 43 – 8
c) 17. (- 85) + 17. 85
Câu 2: (1,0 điểm) Tìm x, biết
a) x – 74 = 118
b) 2.x = –20:10
Câu 3: (2,0 điểm)
Có 12 quả cam, 18 quả xoài và 28 quả bơ. Mẹ bảo Lan chia đều mỗi loại quả đó vào các túi quà sao cho mỗi túi đều có cả cam, xoài và bơ. Hỏi lan có thể chia được nhiều nhất mấy túi quà?
Câu 4: (1,5 điểm)
Bản thiết kế một hiên nhà được biểu thị bởi hình sau. Cần phải mua bao nhiêu mét vuông đá hoa để lát phần hiên nhà đó?
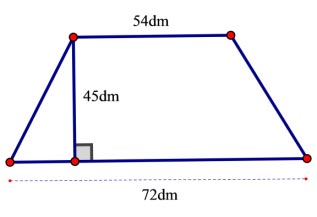
Câu 5: (1,0 điểm): Tìm số nguyên n biết rằng n – 4 chia hết cho n -1
Đề thi học kì 1 môn Toán 6 năm 2022 – 2023 sách Cánh diều
Ma trận đề thi học kì 1 môn Toán 6 năm 2022 – 2023
| Nhận biết | Thông hiểu | Vận dụng | vận dụng cao | Cộng | |||||
| TN | TL | TN | TL | TN | TL | TN | TL | ||
| Chương 1. Số tự nhiên. | |||||||||
| Số câu | 1 | 1 | 2 | 4 | |||||
| Số điểm | 0,5 | 1,5 | 2 | 4 | |||||
| Số câu/ Hình thức | 1 | 5 | 8a, 8b | ||||||
| Thành tố năng lực. | GT | TD | GQVĐ | ||||||
| Chương 2. Số nguyên. | |||||||||
| Số câu | 1 | 2 | 2 | 5 | |||||
| Số điểm | 0,5 | 1,5 | 1 | 3 | |||||
| Số câu/ Hình thức | 2 | 6a, 7a | 6b,7b | ||||||
| Thành tố năng lực. | MHH | MHH | MHH | ||||||
| Chương 3. Hình học trực quan. | |||||||||
| Số câu | 2 | 1 | 2 | 5 | |||||
| Số điểm | 1 | 1 | 1 | 3 | |||||
| Số câu/ Hình thức | 3,4 | 9 | 10a, 10b | ||||||
| Thành tố năng lực. | TD | CC | MHH, CC, GQVĐ | ||||||
| Tổng điểm | 2 | 3 | 4 | 1 | 10 | ||||
Đề thi học kì 1 môn Toán 6 năm 2022 – 2023
| PHÒNG GIÁO DỤC HUYỆN…. TRƯỜNG TH&THCS…… |
ĐỀ KIỂM TRA HỌC KÌ I NĂM 2022 – 2023 MÔN TOÁN 6 Thời gian làm bài : 90 phút |
PHẦN 1. TRẮC NGHIỆM
Chọn đáp án đúng.
Câu 1. 38 đọc là:
A. Tám mũ ba
B. Ba mũ tám
C. Tám nhân ba
D. Ba nhân tám
Câu 2: Số nguyên chỉ năm có sự kiện “Thế vận hội đầu tiên diễn ra năm 776 trước công nguyên” là số nào trong các số sau đây?
A. – 1776
B. 776
C. – 776
D. 1776
Câu 3. Hình nào dưới đây là hình tam giác đều?

Câu 4: Hình nào dưới đây có trục đối xứng?
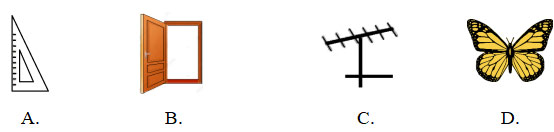
PHẦN 2. TỰ LUẬN
Câu 5: Trong các số 1930, 1945, 1954, 1975. Những số nào chia hết cho 5? Vì sao?
Câu 6: Một chiếc tàu ngầm đang ở độ cao -47 m so với mực nước biển. Sau đó tàu ngầm nổi lên 18 m.
a) Viết phép tính biểu thị độ cao mới của tàu ngầm so với mực nước biển.
b) Tính độ cao mới của tàu ngầm so với mặt nước biển.
Câu 7: Bản tin dự báo thời tiết dưới đây cho biết nhiệt độ thấp nhất và nhiệt độ cao nhất ở Thủ đô Mát-xcơ-va của Liên bang Nga (tính theo độ C) trong các ngày từ 17 / 1 / 2021 đến 23 / 1 / 2021
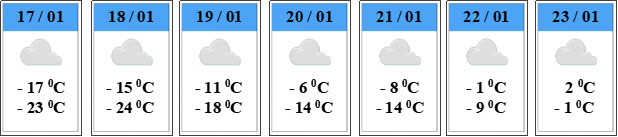
a) Nêu nhiệt độ cao nhất, nhiệt độ thấp nhất ở Thủ đô Mát-xcơ-va của Liên bang Nga (tính theo độ C) trong ngày 22/1/2021
b) Chênh lệch giữa nhiệt độ cao nhất và nhiệt độ thấp nhất ở Thủ đô Mát-xcơ-va của Liên bang Nga trong ngày 22/1/2021 là bao nhiêu độ C?
Câu 8:
a) Tìm bội chung nhỏ nhất của 18 và 27.
b) Thực hiện phép tính:
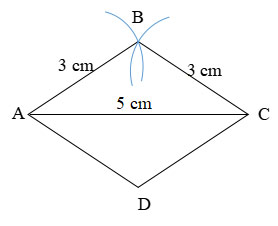
Câu 9: Dùng thước và compa vẽ hình thoi ABCD biết cạnh AB = 3cm, đường chéo AC = 5cm.
Câu 10:
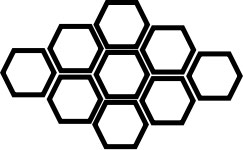
Bạn Hoa sử dụng các ống hút dài 198 mm, để tạo lên hình bên. Mỗi ống hút được cắt thành ba đoạn bằng nhau để tạo lên ba cạnh của mỗi lục giác đều như hình bên.
a) Tính số ống hút bạn Hoa cần dùng để hoàn thành hình bên.
b) Tính tổng chiều dài của tất cả các ống hút mà bạn Hoa đã dùng.
Đáp án đề thi học kì 1 môn Toán 6 năm 2022 – 2023
Câu 1:
– Để trả lời được câu một học sinh phải đọc được biểu thức lũy thừa của một số tự nhiên.
– Câu 1 đánh giá năng lực giao tiếp toán học theo mức độ 1.
– Đáp án: B.
– Điểm số: 0,5.
Câu 2:
– Để trả lời được câu 2, học sinh phải biết sử dụng số nguyên âm để chỉ thời gian trước Công nguyên.
– Câu 2 đánh giá năng lực mô hình hóa toán học theo mức 1.
– Đáp án: C.
– Điểm số: 0,5.
Câu 3:
– Để trả lời được câu 3 học sinh phải nhận biết được tam giác đều.
– Câu 3 đánh giá năng lực tư duy và lập luận toán học theo mức 1.
– Đáp án D.
– Điểm số: 0,5.
Câu 4:
– Để trả lời được câu 4 học sinh phải nhận biết được hình phẳng có trục đối xứng.
– Câu 4 đánh giá năng lực tư duy và lập luận toán học theo mức 1.
– Đáp án: A.
– Điểm số 0,5.
Câu 5:
– Để trả lời được câu 5 học sinh phải biết dựa vào dấu hiệu chia hết cho 5.
– Câu 5 đánh giá năng lực tư duy và lập luận toán học theo mức 2.
– Giải: Trong các số 1930, 1945, 1954, 1975, những số chia hết cho 5 là: 1930, 1945, 1975, vì chúng có chữ số tận cùng là 0 ; 5
– Điểm số: 1,5
Câu 6:
a)
– Để làm được câu 6a, học sinh phải hiểu được vấn đề thực tiễn gắn với thực hiện các phép tính số nguyên.
– Câu 6a đánh giá năng lực mô hình hóa toán học theo mức 2.
– Giải: Phép toán liên quan đến độ cao mới của tàu ngầm dưới mực nước biển là: -47 + 18.
– Điểm số: 0,5
b)
– Để làm được câu 6b học sinh phải giải quyết được vấn đề thực tiễn gắn với thực hiện các phép tính số nguyên.
– Câu 6b đánh giá năng lực mô hình hóa toán học theo mức 3.
– Giải: Độ cao mới của tàu ngầm so với mực nước biển là: -47 + 18 = -29 (m).
– Điểm số: 0,5
Câu 7:
a)
– Để trả lời được câu 7a, học sinh phải hiểu được vấn đề thực tiễn gắn với so sánh hai số nguyên.
– Câu 7a đánh giá năng lực mô hình hóa toán học theo mức 2.
– Giải:
+ Nhiệt độ cao nhất ở Thủ đô Mát-xcơ-va của Liên bang Nga tính theo độ C trong ngày 22/1/2021 là: -10C.
+ Nhiệt độ thấp nhất ở Thủ đô Mát-xcơ-va của Liên bang Nga tính theo độ C trong ngày 22/1/2021 là: -90C.
– Điểm số: 1.
b)
– Để trả lời được câu 7b, học sinh phải giải quyết được vấn đề thực tiễn gắn với thực hiện các phép tính số nguyên.
– Câu 7b đánh giá năng lực mô hình hóa toán học theo mức 3.
– Giải:
Chênh lệch giữa nhiệt độ cao nhất và nhiệt độ thấp nhất ở Thủ đô Mát-xcơ-va của Liên bang Nga trong ngày 22/1/2021 là: -1 – (-9) = 80C.
– Điểm số: 0,5
Câu 8:
a)
– Để làm được câu 8a, học sinh phải xác định được bội chung nhỏ nhất của hai số tự nhiên.
– Câu 8a, đánh giá năng lực giải quyết vấn đề toán học theo mức 3.
– Giải:
Phân tích 18 và 27 ra thừa số nguyên tố:
18 = 2 . 3 . 3 = 2 . 32
27 = 3 . 3 . 3 = 33
BCNN(18, 27) = 2 . 32 = 2 . 27 = 54
– Điểm số: 1.
b)
– Để làm được câu 8b, học sinh phải thực hiện được phép cộng phân số bằng cách sử dụng bội chung nhỏ nhất.
– Câu 8b đánh giá năng lực giải quyết vấn đề toán học theo mức 3.
– Giải:
BCNN(18, 27) = 54
54 : 18 = 3
54 : 27 = 2
– Điểm số: 1.
Câu 9:
– Để làm được câu 9, học sinh phải biết các bước vẽ hình thoi khi biết độ dài cạnh và độ dài một đường chéo.
– Câu 9 đánh giá năng lực sử dụng công cụ, phương tiện học toán theo mức 3.
– Giải: (Học sinh không cần trình bày các bước vẽ trong bài làm của mình). Kết quả vẽ được như hình bên.
– Điểm số: 1.
Câu 10:
– Để làm được câu 10 học sinh phải coi mỗi đoạn ống hút biểu diễn một cạnh của lục giác đều, mô tả được một số yếu tố cơ bản của lục giác đều, biết cách tạo lập lục giác đều.
– Câu 10 đánh giá năng lực mô hình hóa toán học, giải quyết vấn đề toán học mức 4.
– Giải:
a) Muỗi hút được cắt thành 3 đoạn bằng nhau để tạo nên ba cạnh của mỗi lục giác đều.
Vậy mỗi lục giác đều cần 2 ống hút.
Trên hình có tất cả 9 lục giác đều, do đó số hút mà bạn Hoa đã sử dụng là:
9 . 2 = 18 (ống hút).
b) Tổng chiều dài của tất cả các ống hút mà bạn Hoa đã dùng là:
18 . 198 = 3564 (mm)
– Điểm số: 1.
> Tải file để tham khảo trọn bộ đề thi học kì 1 môn Toán lớp 6 tại tài liệu tham khảo của freesoftware.vn





